چند نکته درباره فاز بری که در انتهای مطلب دوباره به آن بر میگردیم.

۱- فاز بری [در فیزیک بس ذره‌ای] تنها به مسیر حرکت ذره وابسته است. ربطی به زمان ندارد – تنها مسیر

۲- فاز بری حقیقی است.

۳- چون همه از کره مثال می زنند بیایید فاز بری را در گذر یک ذره روی مسیرهای مختلف کره در نظر بگیریم – پس در گذر از مسیرهای مختلف، فاز بری متناظر به یک عامل فازی مثل γ است.

فاز بری همچون یک فاز هندسی است. یعنی به این ربط دارد که ذره در گذر یک مسیر، در پایان مسیر یک اختلاف فاز کلی با آغاز دارد. این موضوع وقتی بیشتر نمود پیدا می‌کند که این عملیات به صورت بی دررو انجام شود.

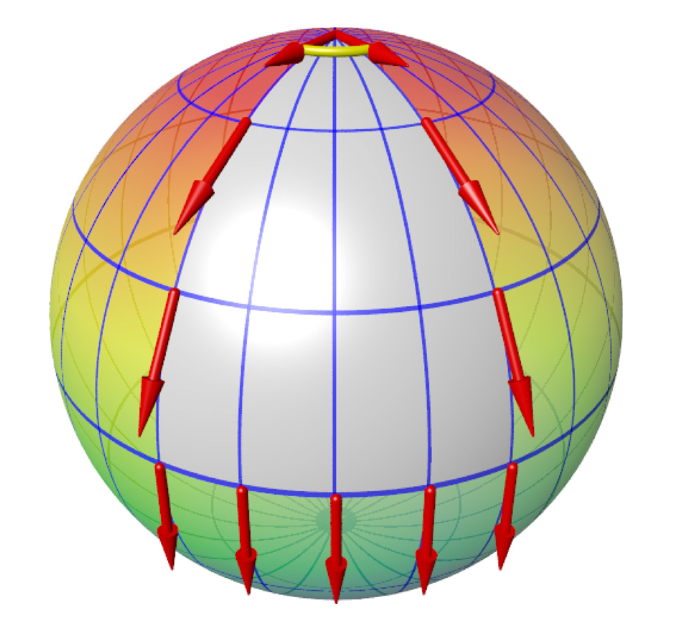
در شکل بالا، ذره از قطب شمال کره با بردار اسپین مشخص شده با سمت پایین آورده میشود – این حرکت به ارامی انجام میشود تا اسپین همیشه مماس بر مسیر (یعنی همان عمل گرادیان) نگه داشته شود.سپس در صفحه x-y خلاف جهت عقربه ساعت به سمت راست برده میشود و در نهایت مماس بر مسیر به قطب برگردانده میشود. جهت بردار در نقطه آغاز و پایان با هم اختلاف دارند (در صورتی که ما خودمان واقعن بردار را نچرخاندیم). این اختلاف فاز همان فاز هندسی یا فاز بری است. فاز بری کمیتی است که کاملا وابسته به مسیر است، یعنی اگر از مسیر دیگری برویم فاز بری متفاوتی به دست می‌آید. عجیب اینجاست که همیشه می گفتیم فاز توابع موج هیچ اهمیتی ندارد و مظهر فیزیکی ندارد. اما این فاز کاملا واقعی است و خودش را به صورت کمیت های قابل اندازه گیری در فیزیک نشان می‌دهد. البته شرایطی هم دارد – مثلن تغییرات روی سامانه به صورت زمانی باید بی دررو باشد و به ذرات فرصت اصلاح حرکتشان متناظر با نیروی خارجی بدهند (مثلن میدان مغناطیسی خارجی) [ که همان تقریب بی دررو یا آدیاباتیک است]. یک مثال از دنیای کلاسیک آونگ فوکو است. مثل فیلم زیر

که آونگ فوکو یک تیله را می اندازد.

مثالی از یک سیستم دو ترازی

فاز بری در یک سیستم دو ترازی زمانی قابل تحقق است که یک الکترون تحت یک میدان مغناطیسی وابسته به زمان قرار گیرد.

B(t) = B (sin θ(t) cos φ(t), sin θ(t) sin φ(t), cos θ(t))

در معادله بالا φ(t) و θ(t) توابعی دوره ای در زمان با یک دوره تناوب یکسان T هستند. فرض کنیم، B(0) = B(T) = B(0,0,1). با تعریف بردار جابجایی تعمیم یافته x(t) = (θ(t),φ(t)) هامیلتونی بی دررو به صورت روبرو می شود: H(x) = −(gμB/h ̄ )B(x) · S

ویژه بردارهای هامیلتونی بالا در زمان t برابر هستند با:

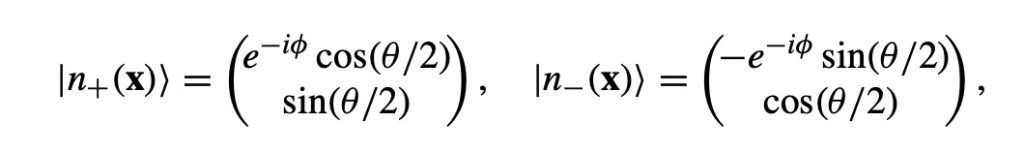
با ویژه مقادیر gμ_BB/2+- در θ = 0, φ = 0 ویژه بردارها

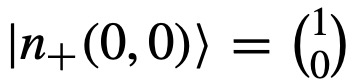
و

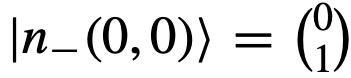
هستند. عبارت های بالا را میتوان در یک ضریب فازی وابسته به جابجایی تعمیم یافته ضرب کرد که وابستگی به مسیر را هم داشته باشد. پتانسیل برداری متناظر با ویژه بردارهای بالا یا همان انحنای بری به صورت زیر میشود:

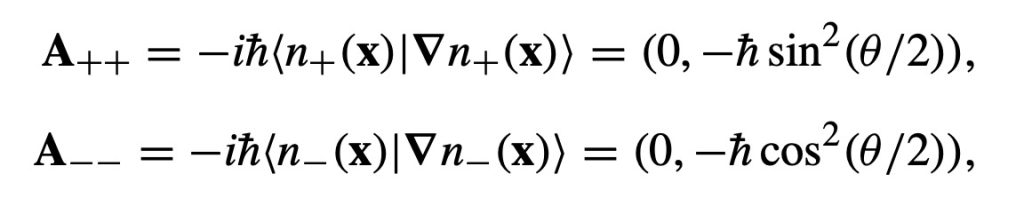
که در آن عملگر

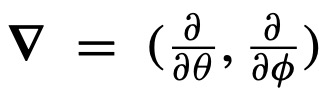
تعریف میشود. بیاییم از |n+(0, 0)⟩ شروع کنیم و میدان را به صورت بی دررو در سه جهت بچرخانیم: ۱- از محور z تا راستای (sin θ, 0, cos θ) اگر θ=π/2 در نظر بگیریم در جهت x قرار میگیرد. ۲- سپس به راستای (0, sin θ, cos θ) می چرخانیم که اگر θ=π/2 در نظر بگیریم در جهت y قرار میگیرد. ۳- در نهایت به همان امتداد محور z بر میگردانیم (0,0,1). اگر این چرخش‌های میدان مغناطیسی آرام باشد اسپین الکترون می‌تواند جهت چرخش را دنبال می‌کند و در این مسیر تابع موج الکترون یک فاز بری به دست می‌آورد.

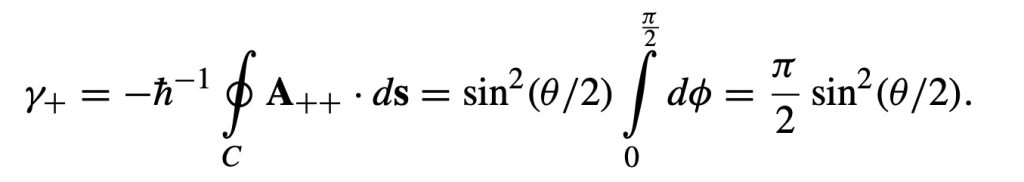
و

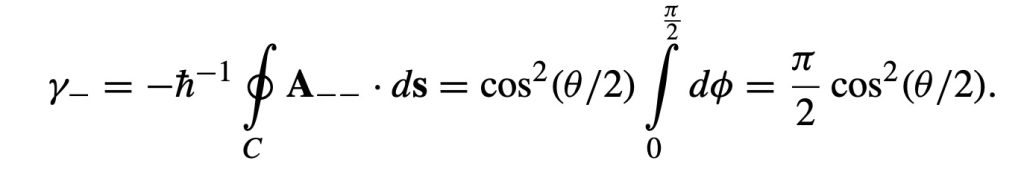
اگر θ = π/2 می بینیم که فاز بری نصف زاویه‌ی فضایی است که به وسیله‌ی منحنی بسته محصور شده است که برابر با γ+ = γ− = π/4 است. زاویه‌ی فضایی متناظر با مساحتی است که بین دو نصف النهار و یک چهارم خط استوا قرار می گیرد که برابر با ۱/۸ زاویه‌ی فضایی یک کره (4π) است یعنی π/2.