شرح دوره
در این آموزش نیز مانند دیگر آموزشهای روی وبسایت، یک کد محاسبات کوانتومی بنام VASP آموزش داده میشود. برای تلف نشدن زمان، ابتدا مقدمات مربوط به کدهای محاسباتی بیان میشود. پس به عنوان یک مرجع آموزشی درباره‌ی نطریه‌های متداول در کدهای کوانتومی این آموزش را مد نظر قرار دهید. همچنین کسانی که در آموزش کدهای دیگر شرکت کرده‌اند، می‌توانند مشترکاً از این بخش استفاده کنند.
کد وسپ نیز مانند دیگر کدهای مبتنی بر شبه پتانسیل و امواج تخت قادر به انجام محاسبات کوانتومی است، اما از نظر امکانات، افزونه‌های مختلف و تکنیک‌های پیاده شده در آن نسبت به دیگر کدها در اولویت قرار دارد. پس از بیان مقدمات و مثالهای متنوع، موضوعات بروز پژوهشی را نیز در این پکیج می‌گنجانیم و دست کم دو کار متمایز پژوهشی را به صورت کامل پوشش می‌دهیم.
گوشزد: آموزشهای کار با کتابخانه‌ی پایتون ASE روزانه به این برگ افزوده میشود.
بخش 1: معرفی و مقدمه
مقدمات مربوط به کدهای محاسباتی (I)
یک تکه بلور از هر ماده‌ای را در دست خود بگیرید. به نظرتان چند عدد الکترون در آن وجود دارد؟ حتما می گویید پاسخش بدیهی است. از مرتبه عدد آووگادرو. اکنون فرض کنید بخواهید معادله‌ی مربوط به این تعداد الکترون، یعنی با این همه درجه آزادی انتقالی را حل کنید. به نظر نشدنی است. حتی فرض کنید مکانیزمی در دست داشته باشید که میتوانید با آن کوپل‌شدگی بین الکترونها را به صورت ظاهری از بین ببرید یا بعبارتی حرکت یک الکترون روی دیگری بی تاثیر باشد. بازهم حل مساله بدون داشتن هیچ تقارنی بی معنی است. پس آیا مکانیزمی برای حل آن وجود دارد؟
فعلا مشهورترین فرمالیسم DFT ( نظریه تابعی چگالی ) است که باید با مفاهیم مربوط به قضیه بلاخ و شرایط مرزی دوره‌ای ترکیب شود. DFT ( نظریه تابعی چگالی ) ذرات را غیربرهمکنشی می‌کند، اما به جای آن ذرات یک محیط دارای اصطکاک (البته نه به معنای کلاسیکی آن که سرعت را کاهش میدهد) ؛یا بهتر بگوییم یک محیط موثر؛ را تجربه می‌کنند. معادله‌ی N ذره‌ای به N تا معادله‌ی تک ذره‌ای کاهش می‌یابد. بعد از اعمال همه چیز بر حسب DFT ( نظریه تابعی چگالی ) نوبت به کاهش تعداد ذرات می‌رسد.
برای فهم بهتر، هر جایگاه اتمی را معادل با یک الکترون در نظر بگیرید. پس N جایگاه، N الکترون دارد و بلور N الکترونی است که N از مرتبه‌ی عدد آووگادرو است. معادله‌ی حاکم بر آن یک معادله‌ی N الکترونی است که با اعمال DFT آن را به N معادله تک الکترونی تبدیل می‌کنیم و از طریق یک کمیت مهم بهم مربوط می‌شوند.
نحوه اعمال قضیه بلاخ به این صورت است که پتانسیل و در نتیجه چگالی الکترونی در یک بلور دوره‌ای، دارای تناوب بلور است ولی خود تابع موج دوره‌ای نیست. شکل تابع موج یک الکترون درون این بلور به صورت زیر است:
\(\psi ({\mathbf {r}})={\mathrm {e}}^{{{\mathrm {i}}{\mathbf {k}}\cdot {\mathbf {r}}}}u({\mathbf {r}})\)
حاصلضرب یک بخش دوره‌ای در یک بخش تخت. بخش دوره‌ای دارای تناوب بلور است:
\( u_n({\mathbf {r+R}}) = u_n({\mathbf {r}}) \)
اندیس n نشان‌دهنده شماره نوار و بخش k عدد موج است که محدود به منطقه‌ی اول بریلوئن (1BZ) است ( مقادیر خارج از منطقه اول معادل با درون منطقه می‌شوند، کافیست تفاضل اعداد موج یک بردار شبکه وارون باشند).
بخش دوره‌ای تابع موج یا حتی پتانسیل دوره‌ای این تصور را ایجاد می‌کند که میتوان آنها را به صورت حاصلجمع امواج تخت نوشت (همان ترکیب سینوس و کسینوس‌ها). به صورت زیر:
\(u_n({\mathbf{r}})=\sum_{\mathbf{G}}{c_{n,\mathbf{G}}}e^{i\mathbf{G}\cdot\mathbf{r}}\)
همین عبارت برای بخش پتانسیل نیز قابل نوشتن است.
اما فرمولبندی‌های فوق، تا زمانی که مفهوم آن را متوجه نشویم، کاملا بی معنی است. شما سیستمی الکترونی در اختیار دارید که دارای بینهایت ذره است. قضیه بلاخ به شما اجازه میدهد تا تنها معادله را به ازای هر k، برای تعداد محدودی الکترون حل کنید. اما باز هم بینهایت عدد موج دارید و باید معادله را به ازای این بینهایت عدد موج، تک تک حل کنید. یا بعبارتی منطقه اول بریلوئن را بروبید. این بینهایت عدد موج با تعداد کل الکترونهای بلور یکسان است.
پس به ازای هر نوار یا (اندیس n) بینهایت عدد موج وجود دارد که با تعداد الکترونها یکسان است. اما تعداد اندیسهای نواری یا n با تعداد الکترونهای درون یک یاخته نسبت دارد. در نتیجه در هر k، تعداد محدودی حالت کوانتومی برای اشغال وجود دارد که این حالت‌های کوانتومی را با n برچسب می‌زنند و با الکترونهای مثلا لایه والانس یکی است (یا حتی نصف آنها).
پس گویا بینهایت الکترون جای خودشان را به بینهایت k داده‌اند. خوشبختانه در اینجا تقریب جایز است. یک نوار پر شده را در نظر بگیرید که دارای بینهایت k در منطقه اول بریلوئن است. در هر k یک تابع موج الکترونی قرار دارد. با تغییر k این تابع موج تغییرات بسیار اندکی چه در قالب پروفایل تابع موج و چه انرژی دارد. یعنی ثابت میشود که پاشندگی انرژی هر نوار دارای حد بالا و پایین است که این بازه خیلی هم بزرگ نیست. پس بجای آنکه منطقه اول بریلوئن را با بینهایت k نمونه برداری کنیم، کافیست نمونه برداری را محدود به تعداد مشخصی k-point کنیم. هم میتوانید انرژی و هم چگالی الکترونی یا هر کمیتی وابسته به k را تا یک آستانه مشخص تعیین کنید.
یک تفاوت بین k و G وجود دارد. k ها همین مقادیری بودند که بخش تخت تابع موج را میساختند.
اما در مورد G:
وقتی پتانسیل یا تابع موج را برحسب امواج تخت بسط می‌دهید، مولفه‌های فوریه‌ای G را وارد بسط می‌کنید. هر چقدر نوسانات بخش دوره‌ای در فضای واقعی یا مستقیم بیشتر باشد، به مولفه‌های بیشتری برای توصیف آن نیاز دارید و ضرایب بسط برد بیشتری دارند. اما یک بیشینه برای هر سیستمی که توصیف می‌کنید وجود دارد که به آن GMax یا Ecut می‌گویند. نوسان کمتر بخش دوره‌ای تابع موج معادل با عدم نیاز به GMax بزرگتر است، و محاسبات سبکتر است.
برای یادآوری یک موج مربعی متناوب را با بسط تخت ایجاد کنید.
در جلسات آینده شکل دقیق معادلات کان-شم و شیوه معمول حل و رفتار با آنها را دنبال می‌کنیم.
معادله‌ی بس ذره‌ای یا معادله‌ی تک ذره‌ای؟
ظاهر تابع موج یک سامانه‌ی برهمکنشی بس ذره‌ای به صورت زیر است:
\(\mathbf{\Psi}= \mathbf{\Psi}(\mathbf{r_1}, \mathbf{r_2}, … , \mathbf{r_N}; \mathbf{R_1} , \mathbf{R_2} , … , \mathbf{R_N}) \)
فرض کنید می‌خواهید مساله را برای بلور سیلییم با ساختار الماسی درون یاخته‌اش حل کنید.
ثابت شبکه این بلور 5.43 آنگستروم و حجم یاخته \(\frac{a^3}{4}\) است. اگر مشبندی یاخته را روی \(\Delta{x}=0.1A\) قرار دهید، گرید درون یاخته شامل \(N_P=\frac{\frac{a^3}{4}}{\Delta{x}}\sim 4000\) نقطه است. مجموع تعداد هسته‌ها و الکترونهای درون این یاخته هم برابر با \(N+M=10\)تاست. اگر از دیدگاه دامنه‌ی احتمال یافتن ذرات به آن نگاه کنید برای تعیین کامل \(\mathbf{\Psi}=\mathbf{\Psi}(\mathbf{r_1}, \mathbf{r_2}, … , \mathbf{r_8}; \mathbf{R_1} , \mathbf{R_2}) \) باید \((N_P)^{10} \sim 10^{46} \) عدد مختلط را در حافظه رایانه ذخیره کنید. بعلاوه اینها را که کنار بگذارید ابعاد ماتریس‌های عملگری چندین برابر افزایش می‌یابد و ضرب ماتریسی بین این عملگرها و آرایه‌ها غیرممکن میشود. سایز سامانه را هم افزایش دهید تعداد محاسبات به صورت نمایی افزایش می‌یابد. برای گذر از این دیوار نمایی راه‌های مختلفی پیشنهاد شده که فراگیرترین آن نظریه‌ی تابعی چگالی است.
البته استفاده از این روش برای محاسبات اتمی خیلی هم بد نیست.
در محاسبات بس‌ذره‌ای دیدیم که برای تعیین کامل تابع موج به تعداد \((NUMGRID)^N\) عدد باید ذخیره کنید. برای ساده‌سازی هسته‌ها را فریز کنید چون جرم بینهایتی نسبت به الکترونها دارند. اما به هرحال این هسته‌ها تابع موج بس الکترونی را با اعوجاج مواجه می‌کنند (فاز بری – اثر جان تلر). پس از تقریب CALMPED NUCLEI برای جداسازی بخش هسته‌ای و الکترونی استفاده میشود و شما دیگر یک معادله‌ی بس الکترونی خواهید داشت. البته این صرفاً یک تقریب است چون از اصل عدم قطعیت می‌دانیم که جایگزیدگی کامل در مکان بی معنی است.
در مرحله بعد از تقریب الکترون مستقل برای نوشتن تابع موج کلی سامانه به صورت حاصلضرب تابع موج تک ذره‌ها استفاده کنید (independent electron approximation)- اما در تقریب الکترون مستقل یک مشکل وجود دارد که باید مرتفع شود: باید جمله‌ی برهمکنش کولنی و اصل طرد پائولی را وارد هامیلتونی کنیم. دترمینان اسلیتر و تقریب MEAN-FIELD پاسخ‌های این مساله هستند. با اضافه شدن پتانسیل هارتری، نوبت به پتانسیل تبادلی و همبستگی می‌رسد که هدف نظریه‌ی DFT است.
پس از اعمال نظریه‌ی تابعی چگالی به مساله‌ی غیربدیهی بس‌ذره‌ای، تابع موج کلی سامانه:
\(\mathbf{\Psi}= \mathbf{\Psi}(\mathbf{r_1}, \mathbf{r_2}, …\mathbf{r_N}) = \prod_{i}^N\psi_i(\mathbf{r}_i)\)
شکل عملگری معادلات کان-شم:
\(E(\rho)= T_s[{\psi_i[\rho]}] + E_H[\rho] + E_{XC}[\rho] + E_{ext} \)
بخش تبادلی همبستگی (XC) طرفداران زیادی دارد: LDA-GGA-metaGGA, … هر کدام هم ناشری دارد که میتوانید در اکثر کتابخانه‌های شبه پتانسیلی آنها را بیابید (در ساختن شبه پتانسیل اطلاعات تابعی نیز وارد میشود).
بعد از این همه حرف به این نتیجه می‌رسیم که:
\(\mathbf{\Psi}=\mathbf{\Psi}(\mathbf{r_1}, \mathbf{r_2}, …\mathbf{r_N}) \rightarrow \psi_1(\mathbf{r}), \psi_2(\mathbf{r}), … , \psi_N(\mathbf{r})\)
یعنی
\((NUMGRID)^N \rightarrow N\times(NUMGRID)\)
برای مساله‌ی سیلیکون این تعداد به
\(10\times4000\)
کاهش می‌یابد. البته اگر شرایط مرزی دوره‌ای اعمال نکنید هنوز \(N=10^{23}\) که باید 4000 ضرب شود. برای اتمها و مولکولهای منزوی بسیار ایده‌آل است معادله را غیردوره‌ای حل کنیم. اما بلور هنوز جای صحبت دارد.
منتظر توضیحات بیشتر برای جلسه بعد باشید.
گرید FFT
در دو جلسه پیش قضیه بلاخ + نظریه‌ی تابعی چگالی را شرح دادیم. در این جلسه وقت آن رسیده تا اندکی در مورد منطقه اول بریلوئن و کمیتهایی که باید در آن محاسبه شوند، حرف بزنیم. توابع موج جلسه اول را بیاد بیاورید:
\(\psi_{n}(\mathbf{r})= u_{n}(\mathbf{r})e^{i\mathbf{k}\cdot\mathbf{r}}, \)
عدد موج \(k\) محدود به منطقه اول بریلوئن یا 1BZ است. بخش دوره‌ای تابع موج نیز دارای تناوب شبکه بود:
\(u_n(\mathbf{r}+\mathbf{R})=u_n(\mathbf{r})\)
که \(\mathbf{R}\) نیز یکی از بردارهای شبکه است. پس بخش دوره‌ای تابع موج را میشد به صورت زیر نوشت:
\(u_n(\mathbf{r})= \sum_{\mathbf{G}} c_{n,\mathbf{G}}e^{i\mathbf{G}\cdot\mathbf{r}},\)
و به صورت معادل تابع موج به صورت زیر درمی‌آید:
\(\psi_n(\mathbf{r})= \sum_{\mathbf{G}}e^{i(\mathbf{k}+ \mathbf{G})\cdot\mathbf{r}},\)
جمع روی \(\mathbf{G}\) باید تا بینهایت باشد. اما از نظر محاسباتی مقدور نیست. پس کافیست جای آنرا با تعداد گسسته‌ای از نقاط تعویض کنیم. این نکته را هم در نظر بگیرید که هر چقدر \(\mathbf{k+G}\) بزرگتر باشد، ضرایب \( c_{n,\mathbf{k}+\mathbf{G}} \) کوچکتر میشود. و این خبر خوبی است. کافیست یک کره در فضای وارون در نظر بگیرید که به اندازه‌ی کافی بزرگ باشد، یا ضرایب در فواصل دور به اندازه‌ی کافی به صفر نزدیک باشند. بهتر است به جای GMAX معادل انرژی آن را استفاده کنیم:
\(E_{cut} \ge\frac{1}{2}\vert\mathbf{k}+\mathbf{G}\vert^2,\)
پس اگر می‌خواهید محاسبات کوانتومی انجام دهید، دو مورد را در نظر بگیرید. (1) همگرایی GMAX و (2) همگرایی k-pointها.
مزیت موج‌های تخت به این است که پایه‌های کاملی در فضا ایجاد می‌کند. یعنی همیشه میتوانید با افزایش موج‌های تخت شکل تابع موج اصلی الکترون را بسازید.
پس اگر برایتان سوال است که این مقادیر را چگونه باید انتخاب کرد، به شکل زیر نگاه کنید.
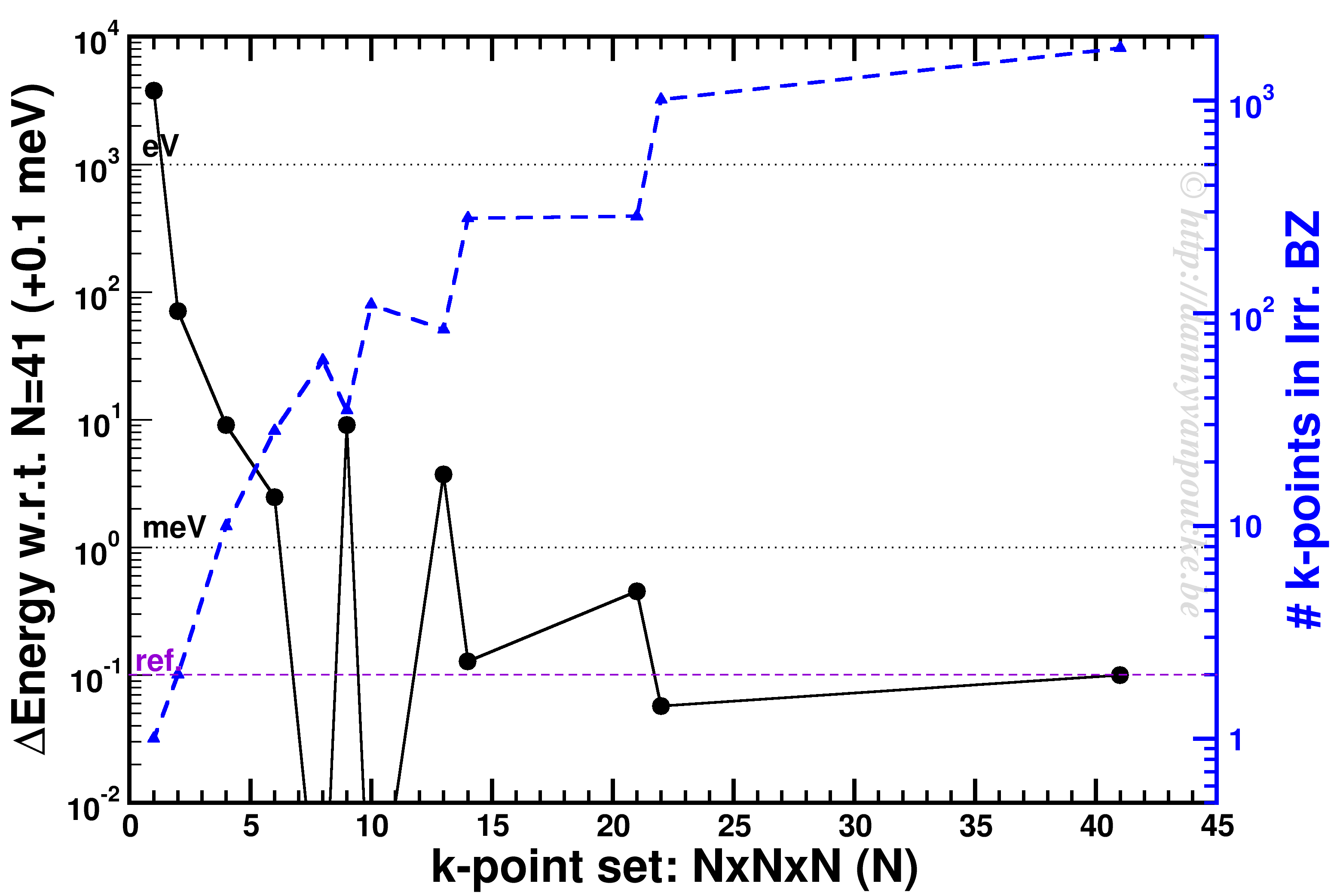
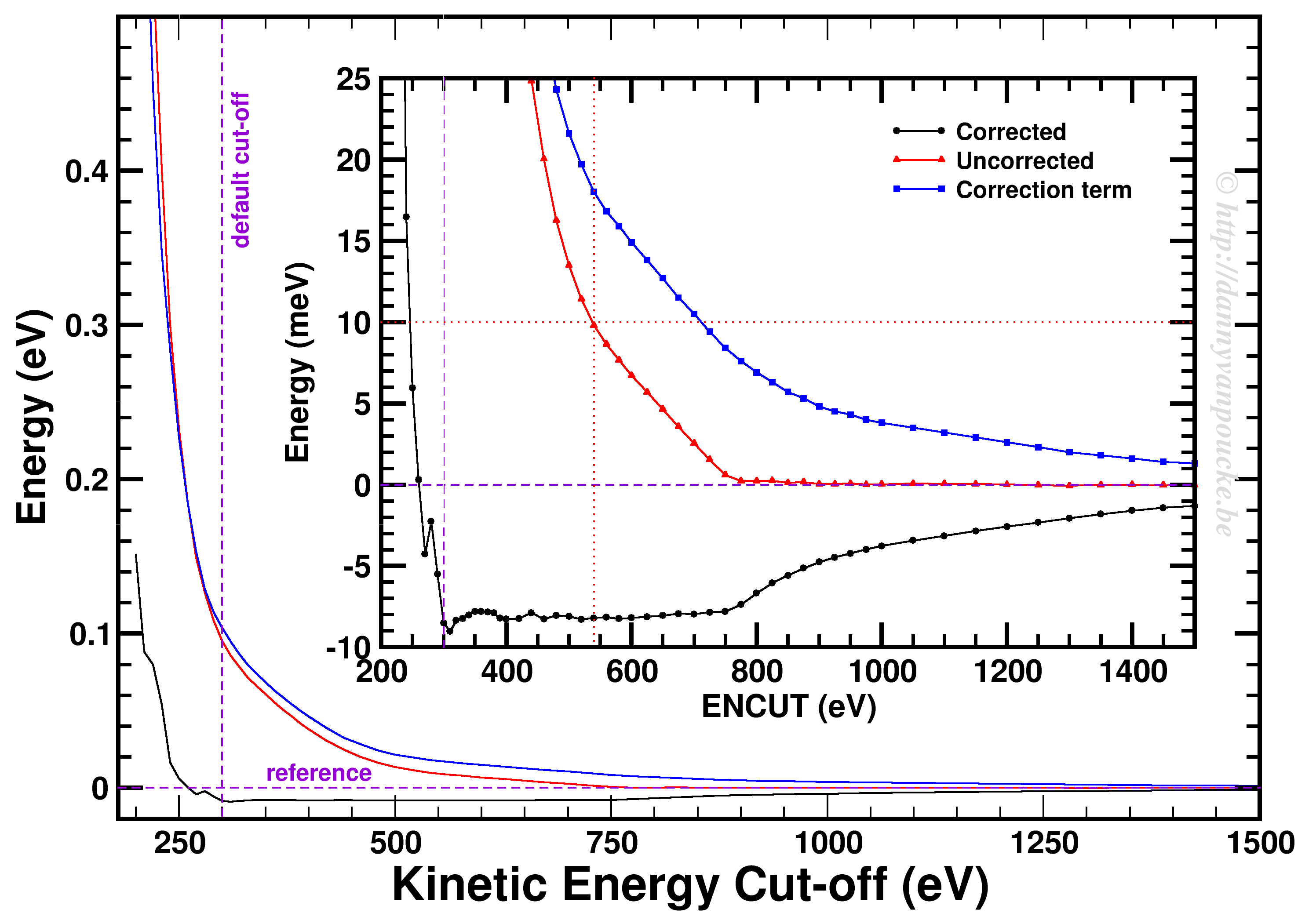
پس دقت محاسبات یک کمیت با استفاده از G-Vector ها و k-point ها به طرز محسوسی قابل تنظیم است. دلیل اینکه از یک کمیت تبدیل فوریه می‌گیرند نیز همین است. با بردن یک کمیت به فضای وارون میتوانید به راحتی ضرایب را انتخاب کنید و ببینید که با افزایش G-vector و kpoint چگونه دقت آن کمیت به دقت مطلوب شما می‌رسد. یکی از این کمیتها که در جلسه پیش هم دیدیم، پتانسیل هارتری است. محاسبه این پتانسیل در فضای متقابل به مراتب ساده تر از فضای مستقیم است.
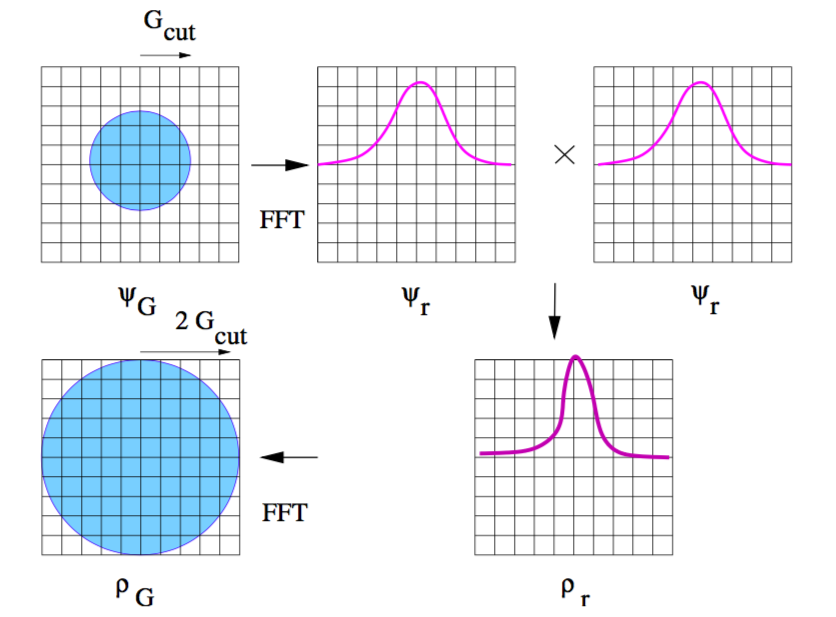
تنها نقطه ضعف، امواج تخت جایی است که نوسانات یک کمیت زیاد میشود. در این صورت به تعداد زیادی موج تخت برای توصیف آن کمیت نیاز است. برای مثال رفتار تابع موج الکترونی در نزدیکی هسته به خاطر داشتن گره و تعامد بشدت نوسانی است. برای اینکه تصویر ذهنی بهتری از نوسانات داشته باشید به تصاویر زیر نگاه کنید:
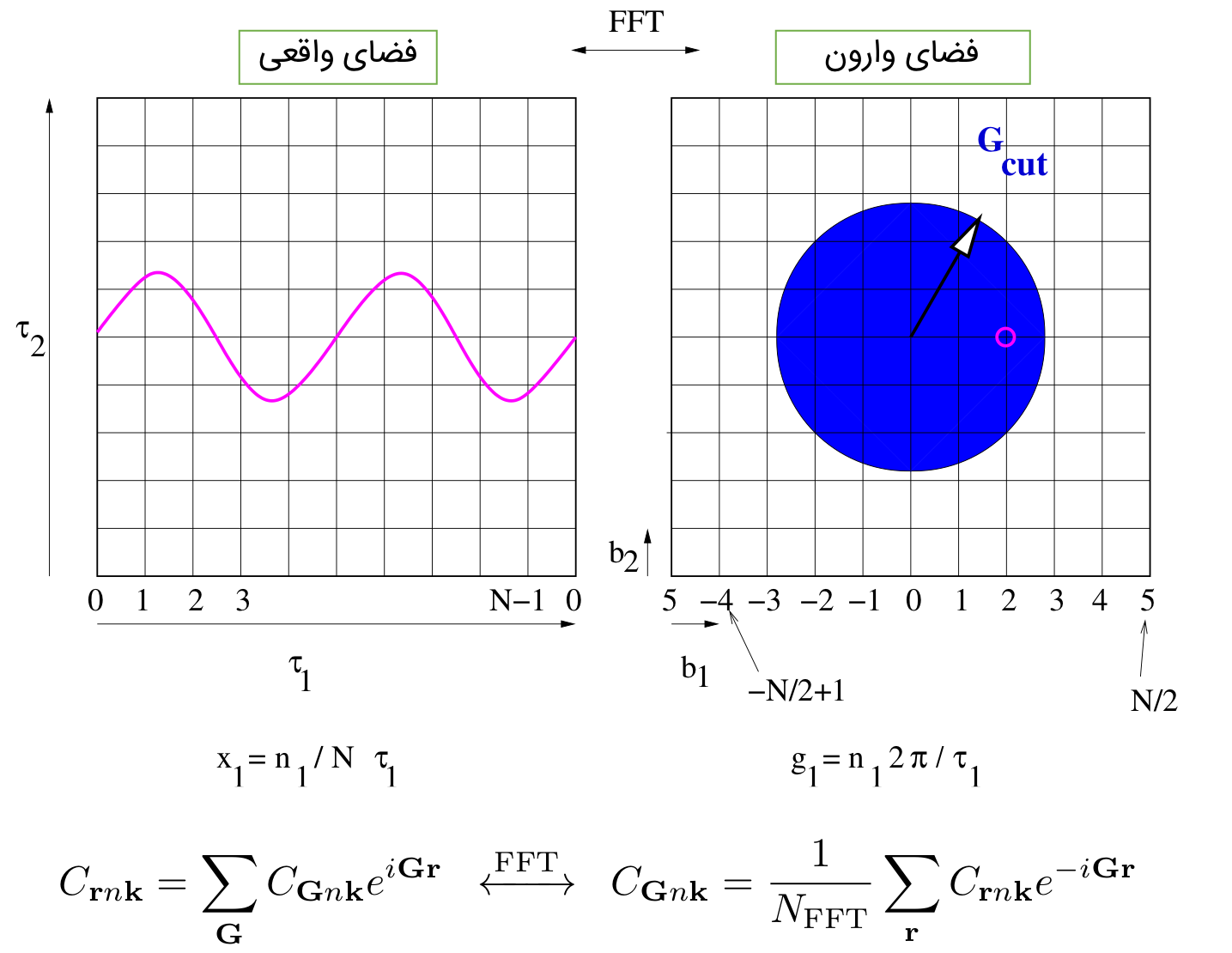
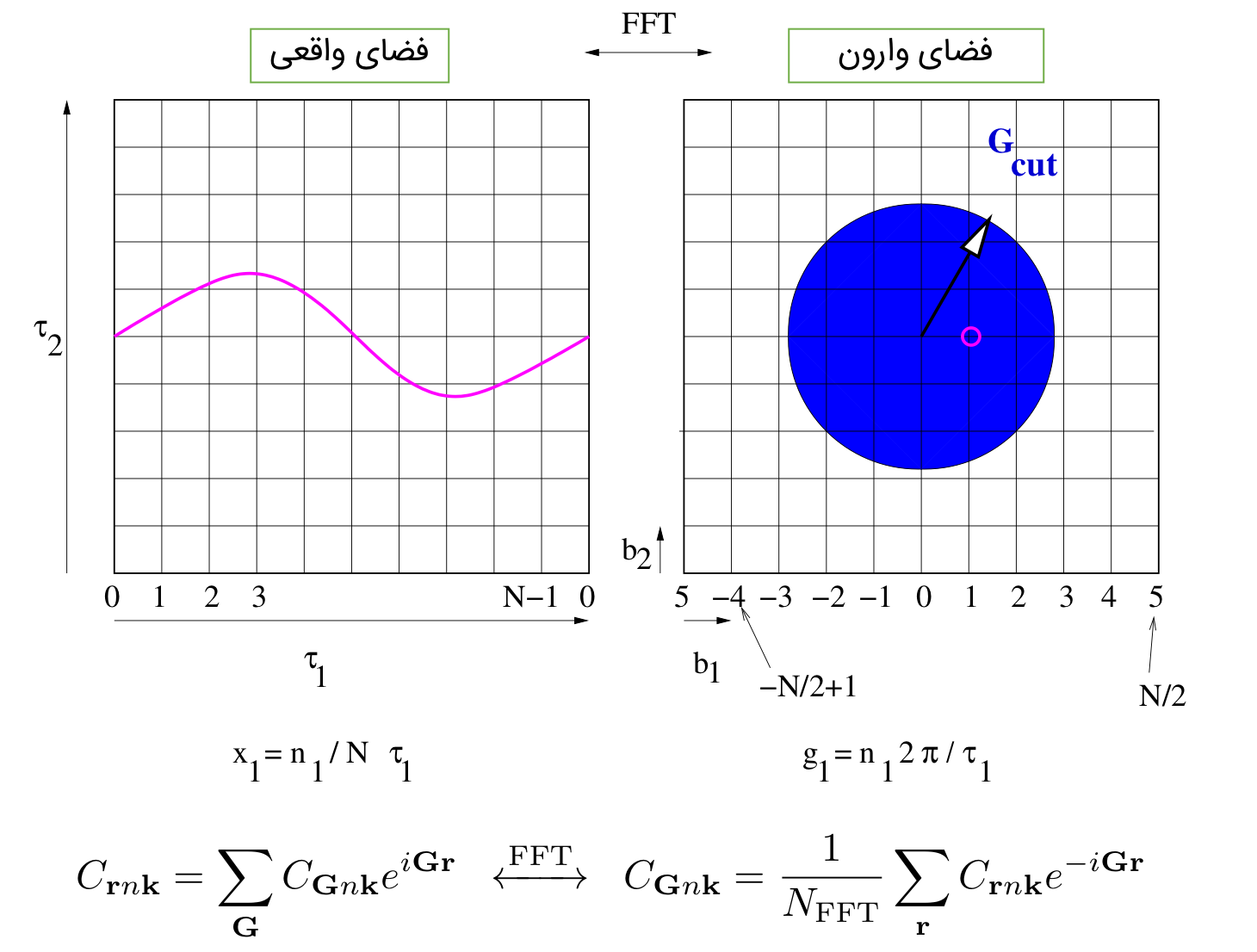
کاملا مشخص است که با افزایش نوسان به گرید (G-VECTOR) با شعاع بزرگتر نیاز دارید.
تصاویر بالا در مورد تابع موج صادق است. اما آیا چگالی الکترونی به انرژی قطع بیشتری نیاز ندارد؟
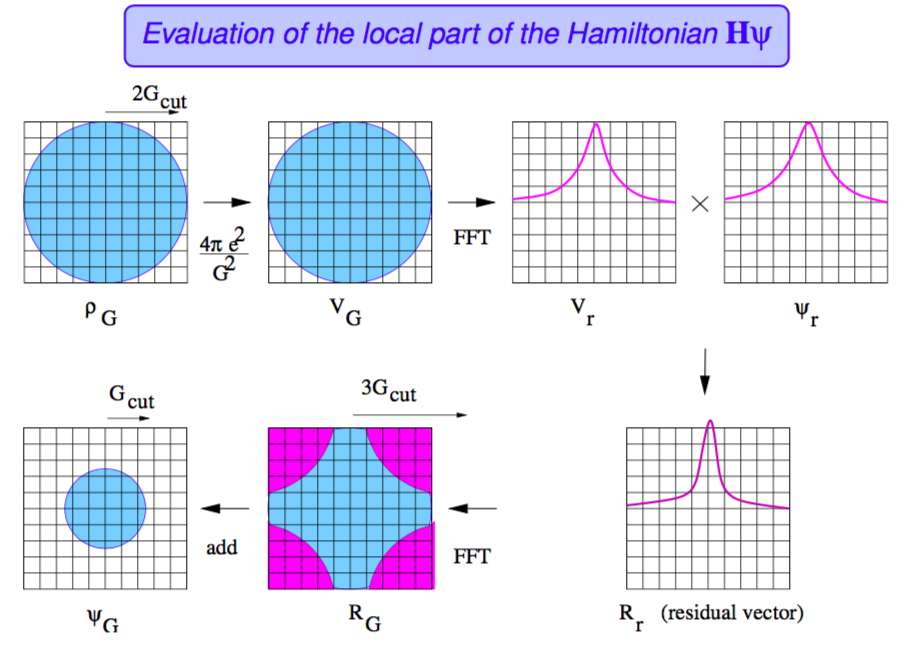
مزیت استفاده از امواج تخت در این است که با اعمال بسیاری از عملگرها روی آنها، بسیار راحت قابل محاسبه اند. برای مثال اثر عمل \(\nabla^2\) را روی امواج تخت در نظر بگیرید.
در حالت کلی عمل \(\mathbf{H}\mid\psi_{n,\mathbf{k}}\rangle\) با امواج تخت بسیار ساده است:
\(({-\frac{1}{2}\nabla^2+V(\mathbf{r})})\psi_{n\mathbf{k}}(\mathbf{r})\)
انرژی جنشی:
\(\langle\mathbf{G+k}\mid -\frac{1}{2}\nabla^2\mid\psi_{n\mathbf{k}}\rangle=\frac{1}{2}\vert\mathbf{G+k}\vert^2C_{\mathbf{G}n\mathbf{k}} \)
به مجموع همه‌ی پتانسیلها پتانسیل موضعی گفته میشود:
\(V=V_H[\rho]+V_{xc}[\rho]+V_{ext} \)
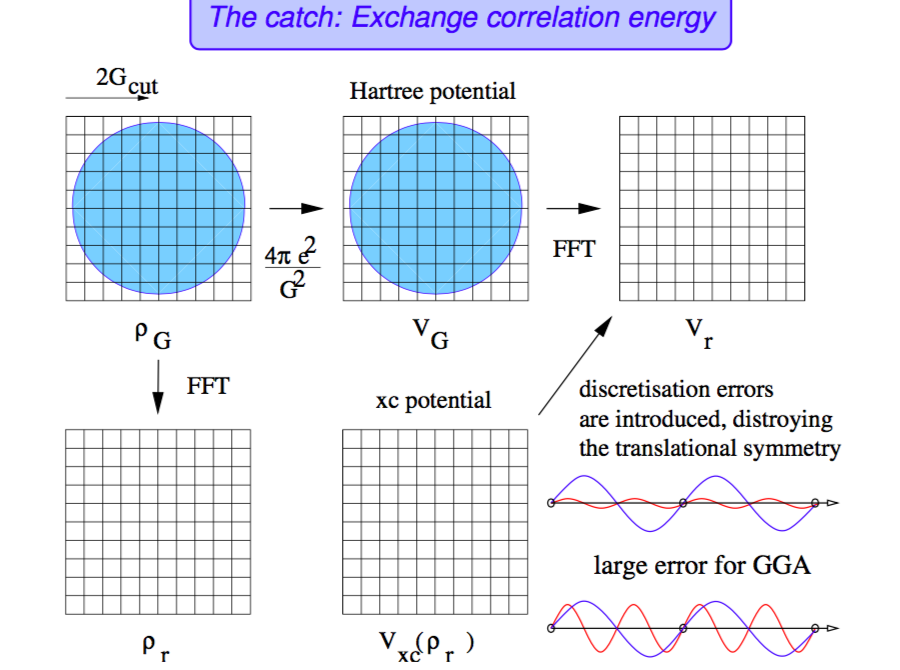
پتانسیل تبادلی همبستگی براحتی در فضای واقعی قابل محاسبه است. هم به دلایل محاسبات عملی و هم محاسبه ساختار نواری همیشه به FFT این کمیت نیاز هست.
از این کمیت FFT گرفته میشود و به فضای وارون منتقل میشود:
\({V_{xc}(\mathbf{r})}\rightarrow {V_{xc,\mathbf{G}}} \)
پتانسیل هارتری: کلا این پتانسیل را فضای وارون راحتتر است و عملا معادل با چگالی است:
\(V_{H,G}=\frac{4\pi}{\vert\mathbf{G}\vert^2}\rho_{\mathbf{G}} \)
پتانسیل موضعی در فضای متقابل به زیر در می‌آید:
\(V_{\mathbf{G}}= V_{\mathbf{H,G}} + V_{xc,\mathbf{G}} + V_{ext,\mathbf{G}}\)
براحتی میتوانید از همه این کمیت FFT وارون بگیرید و آنرا به فضای واقعی برگردانید. اما این همه سختی چه لزومی دارد؟
پاسخ:
محاسبه برخی کمیتها در فضای وارون و FFT گرفتن خیلی سریعتر از محاسبه آنها روی گرید مستقیم است (میتوانید مرتبه کدها را در کتابهای مرجع مختلف پیدا کنید).
حالا سوال پیش می‌آید که جملات فوق با چه ترتیبی محاسبه می‌شوند. برای درک بهتر مراحل طرحواره‌ی حل خودسازگار زیر را در نظر بگیرید که برای همه فرمالیسم‌های DFT یکسان است:
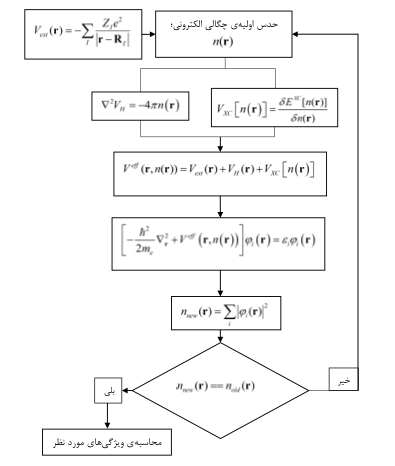
دلیل آن حدس اولیه چگالی را در قضایای هوهنبرگ-کان جستجو کنید.
در بیشتر کدهای محاسباتی برای حدس اولیه چگالی اوربیتالهای اتمی استفاده میشود- مگر آنکه خودتان اوربیتالها را بسازید و برنامه بدهید!!!
مباحث مرتبط با تابعی ها و شبه پتانسیلها نیز در ادامه کار بیان میشود.
تابعی‌های تبادلی-همبستگی Exchange-Correlation Potential + MEAN FIELD APPROX.-POISSON SOLVER
تابعی‌های تبادلی همبستگی Exchange-Correlation Potential + MEAN FIELD APPROX.-POISSON SOLVER – تقریب میدان میانگین
بهتر است کمی درباره‌ی جملاتی که در هامیلتونی بس‌الکترونی ظاهر شدند صحبت کنیم:
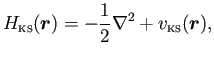
1)جملات تک الکترونی = انرژی جنبشی تک الکترونها ( \(T\)) + انرژی پتانسیل خارجی( \(E_{EXT}\)):
این جملات چیزی شبیه پهنای یک نوار مثلا پهنای نوار 4s (یا با کاراکتر 4S) هستند.
2)انرژی هارتری – پتانسیل هارتری:
از کتاب الکترودینامیک جکسون میتوان به یک دید شهودی و عددی برای محاسبه بخش همبسته و بسیار پیچیده‌ی برهمکنش کولنی الکترونها رسید. کافیست از حرف‌های جلسات پیش بیاد بیاورید که میخواستیم مساله را تک ذره‌ای و غیربرهمکنشی حل کنیم. جوری که الکترونها یکدیگر را نبینند. اینکار با معادله پواسون شدنی است:
\(\nabla^2 V_H(\mathbf{r})=-4\pi n(\mathbf{r}) , \)
پاسخ معادله بالا به شکل زیر است:
\(V_H(\mathbf{r})=\int d\mathbf{r^{\prime}} \frac{n(\mathbf{r^{\prime}})}{\vert \mathbf{r-r^{\prime}}\vert} ,\)
یا عبارتی مشابه برای انرژی:
\(E_H(\mathbf{r})=\int d\mathbf{r} d\mathbf{r^{\prime}} \frac{n(\mathbf{r}) n(\mathbf{r^{\prime}})}{\vert \mathbf{r-r^{\prime}}\vert} ,\)
هر \(d\mathbf{r^{\prime}}\) را یک جعبه بسیار کوچک در نظر بگیرید که دارای بار \(dQ=-n(\mathbf{r^{\prime}})d\mathbf{r^{\prime}}\) است و می‌تواند در نقطه‌ی \(\mathbf{r}\) یک پتانسیل به اندازه‌ی \(\frac{dQ}{\vert \mathbf{r-r^{\prime}}\vert}\) ایجاد کند. با توجه به اینکه متغیر \(\mathbf{r^{\prime}}\) کل فضا را می‌روبد، پس اثر تمامی بارهای درون کل فضای بلور در نقطه \(\mathbf{r}\) به حساب می‌آید. پس عملا هر الکترون، یک پتانسیل میانگین، ناشی همه ابرهای الکترونی را حس می‌کند. به این تقریب MEAN-FIELD-APPROX. گفته میشود. فقط این نکته را در نظر بگیرید که تقریب الکترون مستقل است و مکان قرارگیری یک جعبه روی مکان دیگری تاثیر ندارد. پس اگر در فرمالیسم DFT یک چگالی الکترونی اولیه حدس بزنید (مثلا ATOMIC) باید آنرا درون معادله‌ی پواسون قرار دهید و پاسخ را که پتانسیل هارتری است بیابید.
دوباره باید پتانسیل هارتری را درون معادله شرودینگر قرار دهید و توابع موج جدیدی بدست آورید. این توابع موج جدید، یک چگالی الکترونی جدید به شما می‌دهند که باید دوباره در معادله پواسون قرار گیرد و پتانسیل جدیدی تولید کند. پس عملا این یک سیکل همیشگی است که به آن میدان خودسازگار می‌گویند. برای قطع این سیکل خودسازگار یک شرط خودسازگار روی آن قرار می‌دهند که در بیشتر کدهای محاسباتی به آستانه مشهور است (برای مثال در QE – etot_conv_thr) یا انواع مختلف دیگر آستانه‌ها.
این ساده‌سازی‌ها باید بهایی داشته باشد. همبستگی بین این الکترونها را چطور باید بازیابی کرد؟
نکته پیچیده‌ی دیگر اینست که رقابت بین بخش کولنی و جنبشی باعث میشود که یک الکترون سیار (Itinerant) باشد و دیگری جایگزیده(LOCALIZED) باشد. یعنی این محاسبات باید برای یک نوار صورت گیرد.
به هرحال تصاویری مختلفی در ذهن دانشمندان ایجاد شده است: تصویر الکترونی تقریبا آزاد – تصویر یونی و تصویری مخلوط که بین این دو قرار دارد. مثل سامانه‌های همبسته‌ی قوی.
3)برهمنکش تبادلی: جملات هارتری کاملاً کلاسیکی بود و اجتماعی از بارها را به شکل چگالی الکترونی در نظر می‌گرفت. اما توابع موجی که در تولید این چگالی بار استفاده میشد، می‌بایست دارای یک ویژگی فرمیونی باشند. یعنی تابع موجشان باید از اصل طرد پائولی پیروی کند. اما مشکل اصلی آن در غیر موضعی بودن آن است. یعنی انتگرالده وابسته به دو متغیر فضایی است.
اما معنای برهمکنش تبادلی چیست؟ آیا دو الکترون با اعداد مغناطیسی یا اسپین یکسان می‌توانند یک مکان را اشغال کنند؟
پس در جاهایی که اسپین الکترونها یکی است و توابع موج همپوشانی دارند را باید از پتانسیل هارتری که پیش از این به صورت ناخواسته این برهمکنش ها را وارد کرده، کم کنیم. پس با این کار الکترونهایی با اسپین یکسان همبسته می‌شوند. منطقی است که شکل برهمکنش تبادلی به صورت حاصلضرب دوتابع موج باشد-یعنی همپوشانی را نشان دهد.
پس این نوع الکترونها چون نمی‌توانند کنار هم قرار گیرند، یکدیگر را دور می‌کنند- پس همبسته می‌شوند. به همین دلیل به آن اصل طرد پائولی یا دافعه‌ی پائولی می‌گویند. پس عملاً یک همبستگی مکانیک کوانتومی روی میدهد.
نکته دیگر اینست که عملا این یک برهمکنش نیست و ما برای جبران مشکلات ساده سازی هارتری آن را وارد کرده‌ایم و این ذاتی توابع موج است.
4)پتانسیل همبستگی: الکترونی که در میدان موثر کولنی پواسون حرکت می‌کند، آنهم بی اعتنا به محیط اطرافش، هنوز توصیف درستی نیست. پتانسیل همبستگی می‌خواهد این نقیصه را نیز رفع کند. مثلا یک مورد قابل تصورش را فرض کنید. الکترونی که حرکت می‌کند به خاطر دافعه‌ی کولنی با الکترونهای دیگر آنها را از هم خودش دور می‌کند. آیا در پتانسیل هارتری (پتاانسیلی الکترواستاتیک) آن را به حساب آورده‌ایم؟؟؟ پس این الکترون یک حفره دور خودش ایجاد می‌کند و سعی می‌کند تا یک محدوده‌ی کوتاه (SHORT-RANGED) احتمال حضور دیگر الکترونها را به صفر برساند. اصطلاحاً به آن حفره تبادلی همبستگی می‌گویند. که این حفره‌ها می‌تواند منشاهای فوق‌العاده جذاب و پیچیده‌ای داشته باشد.
اگر پتانسیل تبادلی همبستگی را که مرتبه آن نسبت به دیگر جملات کوچکتر هم هست، بدانیم رفتار جمعی الکترونها دقیقاً قابل پیش‌بینی است. اما این کار خیلی شدنی نیست و خیلی‌ها اعتقاد دارند بسیاری از پدیده‌ها با کاراکتر تک ذره‌ای قابل توجیه نیستند.
————————————
ساده‌ترین تابعی تبادلی همبستگی در DFT، تقریب چگالی موضعی یا LDA است (CEPERLY, ALDER). در این تقریب چگالی انرژی تبادلی همبستگی در هر نقطه‌ای برابر با همتای گاز الکترونی یکنواخت (HEG) است. همین تقریب را میتوان به سامانه‌های اسپینی نیز اعمال کرد (LSDA یا LOACAL DENSITY APPROXIMATION).
انرژی تبادلی همبستگی در تقریب LSDA:
\(E^{LSDA}_{XC}[n_{\uparrow},n_{\downarrow}] = \int n (\mathbf{r}) \varepsilon_{XC}^{LDA} [n_{\uparrow}(\mathbf{r}), n_{\downarrow}(\mathbf{r})]d\mathbf{r},\)
انرژی تبادلی همبستگی به ازای هر الکترون در یک گاز یکنواخت با چگالی اسپینی \(n_{\uparrow}\) و \(n_{\downarrow}\) به شکل زیر بدست می‌آید:
\(\varepsilon_{XC}^{LDA} [n_{\uparrow}(\mathbf{r}), n_{\downarrow}(\mathbf{r})]=\frac{1}{2}\int n(\mathbf{r^{\prime}})(\bar{g}^{HEG}[\vert \mathbf{r} – \mathbf{r^{\prime}}\vert , n\uparrow (\mathbf{r}) , n\downarrow (\mathbf{r})]-1)d\mathbf{r^{\prime}}\)
برای اینکه بهتر بفمیم این عبارت به چه صورتی محاسبه میشود، گاز الکترونی یکنواخت را در نظر بگیرید. انرژی تبادلی این گاز به صورت تحلیلی قابل محاسبه است. اما بخش همبستگی آن با حل معادله بس ذره ای با روشهای آشوبناک بدست می‌آید (\(E_X+E_C\) ). (مونت کارلوی کوانتومی)
اگر چگالی الکترونی در بلور کندتغییر باشد، یعنی نوسانات خیلی شدیدی نداشته باشد، میتوان در هر موضعی به صورت یک مستطیل چگالی‌ها الکترونی بلور را با چگالی الکترونی گاز یکنواخت جایگزین کرد. به این شکل نگاه کنید:
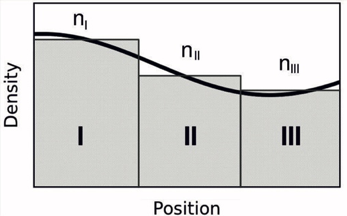
پس طبق این شکل نمیتوان از LDA در سامانه‌های مولکولی و کلاستری استفاده کرد. چون چگالی الکترونی این سامانه‌ها بسیار پرنوسان است.
LDA طول پیوندها را کمتر مقدار تجربی تخمین می‌زند.
تابعی بهتر GGA است که بهترین آن PBE (PERDEW,BURKE & ERNZERHOF) است. در این تقریب شیب چگالی نیز وارد میشود:
\(E^{LSDA}_{XC}[n_{\uparrow},n_{\downarrow}] = \int n (\mathbf{r})\varepsilon_{XC}^{LDA} [n_{\uparrow}(\mathbf{r}), n_{\downarrow}(\mathbf{r}),\nabla n_{\uparrow}(\mathbf{r}) , \nabla n_{\downarrow}(\mathbf{r})]d\mathbf{r},\)
علاوه بر تقریب GGA، در تقریب META-GGA، مشتق دوم چگالی نیز در نظر گرفته میشود.
پس در این جلسه مفاهیمی را یاد گرفتید که نیاز به تحقیق بیشتر و خواندن مقالات بسیار است. باز هم برای درک بهتر میتوانید به LETTER های اصلی ناشرین این تابعی‌ها مراجعه کنید و پارامترهایی که استفاده کرده‌اند را بفهمید و در محاسبات تغییر دهید.
توجه
برای دسترسی به فصل های این دوره باید ابتدا در دوره ثبت نام کنید.
توجه
برای شروع پرسش و پاسخ باید در دوره ثبت نام کنید !
از همین مدرس
محصولات مشابه
وضعیت دوره
دوره درحال برگزاری هست.
250 هزار تومان
حداقل ۱ امتیاز ضروری هست
| 52دانشجو |
| 57 درس |
| آخرین آپدیت : جمعه, 02 دی 1 |
| سطح دوره : پیشرفته |
| زبان : فارسی |
| نوع دوره :غیر حضوری |
| زمان دوره :دست کم ۳۰ ساعت |
| حجم فایل ها : کمتر از ۱ گیگابایت |
| پشتیبانی :تیکت و تلگرام |
| پیش نیاز :پایتون |
| بدون دیدگاه |
| 2129 مشاهده |
| برچسب: vasp نظریه تابعی چگالی وسپ |
| دسته: دوره های برنامه نویسی فیزیک |
| لینک کوتاه دوره: |
مشاوره رایگان
برای کسب اطلاعات بیشتر درباره این دوره درخواست مشاوره خود را ارسال کنید و یا با ما تماس بگیرید.
دیدگاهها
هیچ دیدگاهی برای این محصول نوشته نشده است.